Implementing Gradient Descent to Intelligently Train a Remarkable Multi-Classifier

This is the second entry in my series exploring the fundamentals of machine learning and AI by programming them from scratch. Follow along with the accompanying notebook by clicking here. Previously, I built a binary classifier from scratch, and trained it using a random local search method. It was implemented in such a way that you could watch the weights change from epoch to epoch in a graph. I managed to achieve ~80% accuracy predicting whether customers would make a purchase on an online shop using this method. Check that post out by clicking here. Now, lets move on to the topic of this post: implementing gradient descent from scratch in python.
This time, I wanted to take a step forward: instead of using random local search—small, random updates to the current best set of weights to try to find a slightly better set—I want to train more intelligently, using a method that is guaranteed to result in a set of weights that reduces loss (more on this later) between most epochs. This new method is called gradient descent. But before implementing gradient descent, we need to know what “gradient” we are descending. And for that, we need to understand loss.
Follow along with this post by accessing my notebook.
What is a Loss Function?
In my previous post, I used the accuracy of the model to determine how well the model performed. Each example that my binary classifier labelled incorrectly contributed to a decrease in the accuracy of the model. So to create a model that produced the most correct results, I needed to create a model whose weights and bias made the accuracy as high as possible. I used random local search to perform my parameter updates in that classifier, which meant there was no guarantee that a change to the parameters would result in better model performance.
Fortunately, there is a way to guarantee that every parameter update will improve the performance of the model: through the use of loss and gradient descent. By using gradient descent, we can guarantee that every adjustment we make to the weights will decrease the loss (a measure of our model’s performance, lower loss means higher performance). We can guarantee this through the use of calculus. But, to use calculus, we need a metric that gives us this information while also being continuous and differentiable: a loss function.
We will use one of these, hinge loss, to train our model. The idea of this loss function will be not only to reward the model for placing a high score on the correct label, but also to reward it for assigning a sufficiently high score to the correct label relative to the scores it assigns to the incorrect labels. More on this later.
Fish Species Dataset
Now, let’s move on to exploring our dataset. The fish species dataset contains data about the length, weight, and species of particular fish specimens:
- species: name of the species.
- length: length of specimen, in centimeters.
- weight: weight of specimen, in grams.
- weight-to-length ratio: weight of specimen divided by length of specimen.
So, the dataset we will use has 3 feature columns, a single label, and every column except the label is numeric:
| species | length | weight | w_l_ratio |
| Anabas testudineus | 10.66 | 3.45 | 0.32 |
| Anabas testudineus | 6.91 | 3.27 | 0.47 |
Inference Prep Work
Now that we understand the structure of our data, we need to prep the dataset for our classification task. Similarly to my binary classifier, I divided my data into training and test set, and normalized my columns using the training set. This time around, however, I decided to do two things differently:
Validation Set
Firstly, I decided to use a validation set for this inference task. A validation set is an extra set of data that is partitioned from the full data set in addition to the training and test sets. It is mainly used to tune the hyperparameters of the model, such as learning rate or batch size, to achieve optimal performance. In this example, I decided to use 70% for training, 10% for validation, and the remaining 20% for testing:
train = reg.sample(frac=0.7)
rest = reg.drop(train.index)
test = rest.sample(frac=0.6666)
val = rest.drop(test.index)Bias Trick
The other change I made from my previous method was making use of the “bias trick”. This basically means folding the bias term into the weights vector so that an entire inference task can be performed using only a single matrix multiplication step. So, instead of using
y = wx + b
to apply our weights and bias to an example, by adding the bias term onto the end of the weights matrix we get
y = mx
The astute mathematicians among you will notice that if we add bias onto the weights matrix, that will change the matrix dimensions, thereby making it impossible to use matrix multiplication between the weights and a batch of samples for the prediction step. Luckily, the other half of the bias trick comes in to solve this problem. Step two of the bias trick is to add an extra column to x, with a value of 1. This can be done relatively simply:
reg['bias'] = 1This rectifies the dimensionality issue, enabling matrix multiplication, and it also guarantees that bias will be treated as a constant, because
b * 1 = b
So, the bias trick will simplify our equations and allow us to take a step out of the python implementation of our model.
Support Vector Machines
If you take the time to dig in to the fish species dataset, you will notice that there are 9 different species of fish represented. This means that our classifier will need to be able to make its choice between nine options instead of just two like in a binary classifier.
This can be achieved in a variety of ways. One such way is through the use of a concept known as a Support Vector Machine, or SVM. The idea of an SVM is this: the goal is to find a “hyperplane” that maximally separates examples of different classes. For example, in 2D space, a this hyperplane of maximum separation might look like this:
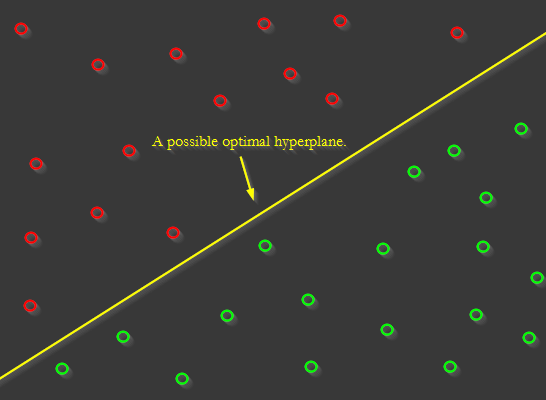
In higher-dimensional data, instead of a line, imagine a flat plane separating the classes. Our goal with a Support Vector Machine is to find the weight and bias values that define that plane. Then, we can use those values to make predictions about whether a sample corresponds to a particular class.
Because there are more than 2 class labels in our dataset, there will be multiple hyperplanes dividing the classes in our data. Thus, we will need to find a set of weights and biases to define each of them.
Model Pseudo Code
Before moving any further, I want to define the basic structure of the model class. This is the class I will use to make predictions, calculate loss, and train my model using gradient descent. This is preview of the my SVM class, with no implementations of the methods yet:
class SVM:
def __init__(self):
pass
def predict(self, X):
'''
returns class predictions in np array of size
n x m, where n is the number of examples in X
and m is the number of classes
'''
pass
def loss(self, scores, y, delta=1):
'''
returns the average hinge loss of the batch
'''
pass
def gradient(self, scores, X, y, delta=1):
'''
returns the gradient of the loss function
'''
pass
#divide the gradient by number of examples to get the average gradient
return gradient / len(X)
def fit(self, X, y, epochs = 1000, batch_size = 256, lr=1e-2, verbose=False):
'''
trains the model on the training set
'''
passImplementing the Classifier
Let’s step through the implementation of the SVM Multi-classifier one method at a time.
__init__
The constructor has one main purpose: to initialize the weights and biases of the model. To do this correctly, there are two facts that we need to recall:
- We are using the bias trick.
- We need to define a classifier for each possible class in the dataset.
This means that we need to create a matrix of randomly-initialized numbers of size n by m + 1, where n is the number of possible classes, and m is the number of features. We add one to m because we need to add a bias value to the matrix for the bias trick. This will result in n sets of weights (one for each class), and each set will contain m weights and a bias (one for each attribute of the data, plus the bias). I do that like this:
class SVM:
def __init__(self):
self.weights = np.random.randn(len(labels), X_train.shape[1]) * 0.1
self.history = []I also define a list called history, which I will use to track training progress. This is used to plot the progress visually to make sure everything is working properly.
predict
This is the meat and potatoes of our classifier! It is the method that applies the weights and biases to a set of examples to predict the labels for those examples. Fortunately, this is implemented very simply! All we need to do is a simple matrix multiplication of self.weights with the set of examples passed in, X. Because self.weights is a n by m + 1, and X is of size len(X) by m+1, we need to transpose X to make the weights match with the example values properly. This will result in a matrix with dimensions n by len(X). Then, we just transpose matrix again to re-establish len(X) as the first dimension.
def predict(self, X):
#matrix multiplication to apply weights to X
bounds = self.weights @ X.T
#return the predictions
return np.array(bounds).TThe result of this function is an array where each row is vector of n numbers, where a higher number at an index means the classifier views this class label as more likely than a lower value at another index.
loss
This function calculates the hinge loss of the model’s predictions for a specific set of examples. Hinge loss is defined by the function:
![Li=∑j≠yi[max(0,wTjxi−wTyixi+Δ)]](https://jacob-t-graham.com/wp-content/uploads/2024/10/image-1.png)
Where wj_xi is the prediction for each incorrect class, and wyi_xi is the prediction for the correct class for an example xi. Delta is an integer, usually simply set to 1.
This function calculate the difference between the score assigned to the incorrect class and the correct class, then adds delta. What happens then depends on value result of that operation, r:
- If r > 0, then wj_xi + 1 > wyi_xi, meaning that the incorrect class was not scored lowly enough. Loss increases by r.
- If r <= 0, then wj_xi + 1 <= wyi_xi, meaning the incorrect class was scored sufficiently low. Loss does not increase.
This operation is done for each incorrect class, and the totals are summed to get the loss for a particular sample. For a batch, we simply average this loss across all examples in the batch. In code, it looks like this:
def loss(self, scores, y, delta=1):
#calculate the loss for a prediction and corresponding truth label
total_loss = 0
#compute loss for each example...
for i in range(len(scores)):
#extract values for this example
scores_of_x = scores[i]
label = y[i]
correct_score = scores_of_x[label]
incorrect_scores = np.concatenate((scores_of_x[:label], scores_of_x[label+1:]))
#use the scores for example x to compute the loss at x
wj_xi = incorrect_scoresscores
wyi_xi = correct_score
wy_xi = wj_xi - wyi_xi + delta
losses = np.maximum(0, wy_xi)
loss = np.sum(losses)
#add to the total loss
total_loss += loss
#return the loss
avg_loss = total_loss / len(scores)
return avg_lossThis function takes in the predictions for each class produced by predict, and the ground truth labels, and returns a number: the loss for the provided examples.
gradient
The gradient method is where the work of calculating the step, or adjustment to make to the weights, is done. There are two ways to do this: numerically and analytically. Computing the gradient numerically is simple and easy to understand. All you have to do is choose a datapoint that is very slightly different from the current datapoint, and compute the change in the prediction divided by the change in the inputs. The problem with this method is, it is slow in code implementations, and it does not give the exact answer.
That brings us to the second method: computing the gradient analytically. This is done by calculating the derivative of the loss function with respect to the weights of the model. Because we are using the derivative, this method gives us exactly the right direction to adjust each of the weights to guarantee a reduction in loss. It returns, if you will, the slope of the hyperplane at a given point in multidimensional space. Once we have that, all we need to do is step “downhill” in the direction that reduces loss.
So, we need to take the derivative of the loss function in order to find the gradient. The derivative of the hinge loss function is
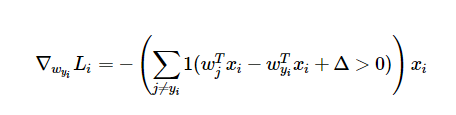
where 1 is the indicator function. In practice, what this function does is count how many of the incorrect classes were not assigned satisfactorily low scores for a given example, multiply that count by -1, and then multiply the example (xi) by that number. This gives the adjustments that should be made for the set of weights that correspond to the correct class.
Meanwhile, for each incorrect classifier’s weights, the gradient is calculated using
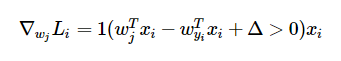
This function works very similarly to the previous function. It returns 0 if class j was assigned a sufficiently low score, and 1 otherwise. It then multiplies the example (xi) by that number, which determines whether the weights for incorrect classifier j should b changed at all.
In code, these calculations look like this:
def gradient(self, scores, X, y, delta=1):
#calculate the loss and the gradient of the loss function
#gradient of hinge loss function
gradient = np.zeros(self.weights.shape)
#calculate the gradient in each example in x
for i in range(len(X)):
#extract values for this example
scores_of_x = scores[i]
label = y[i]
x = X[i]
correct_score = scores_of_x[label]
incorrect_scores = np.concatenate((scores_of_x[:label], scores_of_x[label+1:]))
### start by computing the gradient of the weights of the correct classifier
wj_xi = incorrect_scoresscores
wyi_xi = correct_score
wy_xi = wj_xi - wyi_xi + delta
losses = np.maximum(0, wy_xi)
#get number of nonzero losses, and scale data vector by them to get the loss
num_contributing_classifiers = np.count_nonzero(losses)
g = -1 * x * num_contributing_classifiers
#add the gradient of the correct classifier to the gradient
gradient[label] += g
### then, compute the gradient of the weights for each incorrect classifier
for j in range(len(scores_of_x)):
#skip the correct score, since we already did it
if j == label:
continue
wj_xi = scores_of_x[j]
wyi_xi = correct_score
wy_xi = wj_xi - wyi_xi + delta
loss = np.maximum(0, wy_xi)
#get whether this classifier contributed to the loss,
#and scale the data vector by that to get the gradient
contributed_to_loss = 0
if loss > 0:
contributed_to_loss = 1
g = x * contributed_to_loss
#add the gradient of the incorrect classifier to the gradient
gradient[j] += g
#divide the gradient by number of examples to get the average gradient
return gradient / len(X)This function applies the previously mentioned derivatives to create a matrix of the same size as the classifier’s weights. It adds the gradient for each element in X elementwise to the gradient, then divides by the total number of examples in X to get the average gradient of the batch.
Note: as you may be able to tell, it would likely be more efficient to calculate loss and gradient together in a single function, as they both involve a lot of the same work. I am aware of this, but wanted to separate them for a clear separation of concerns.
fit
Fit is where the training magic happens! All the previous parts come together here to find the weights and biases that best predict which species of fish our example is. In short, it is where we will be Implementing gradient descent! The steps in fitting the model to the training data are:
- Create a batch of data from the training set.
- Have the model make a prediction on the data.
- Calculate the loss (how well the model predicted the data).
- Calculate the gradient of the loss function for the batch.
- Use the gradient to calculate the step to take.
- Perform the parameter update in the negative direction (to descend the gradient).
- Repeat until satisfied.
With that in mind, lets take a look at a code implementation of fit. The steps are labeled in comments.
def fit(self, X, y, epochs = 1001, batch_size = 256, lr=1e-2, verbose=False):
# 7.gradient descent loop
for epoch in range(epochs):
self.history.append({'epoch': epoch})
# 1. create a batch of samples to calculate the gradient
#NOTE: this significantly boosts the speed of training
indices = np.random.choice(len(X), batch_size, replace=False)
X_batch = X.iloc[indices]
y_batch = y.iloc[indices]
X_batch = X_batch.to_numpy()
y_batch = y_batch.to_numpy()
# 2. evaluate class scores on training set
predictions = self.predict(X_batch)
predicted_classes = np.argmax(predictions, axis=1)
if epoch%50 == 0 and verbose:
print(f"pred: {predicted_classes[:10]}")
print(f"true: {y_batch[:10]}")
# 3. compute the loss: average hinge loss
loss = self.loss(predictions, y_batch)
self.history[-1]['loss'] = loss
#compute accuracy on the test set, for an intuitive metric
accuracy = np.mean(predicted_classes == y_batch)
self.history[-1]['accuracy'] = accuracy
if epoch%50 == 0 and verbose:
print(f"Epoch: {epoch} | Loss: {loss} | Accuracy: {accuracy} | LR: {lr} \n")
# 4. compute the gradient on the scores assigned by the classifier
gradient = self.gradient(predictions, X_batch, y_batch)
# 5. backpropagate the gradient to the weights + bias
step = gradient * lr
# 6. perform a parameter update, in the negative direction of the gradient
self.weights -= stepAs you can see, the training loop is actually not too complicated. The only extra steps are saving key training metrics to the self.history list. These will be used for graphing progress later.
Test Set Result
After that, the class is complete! Each method has been fully implemented, and we are ready to start classifying fish specimens. All I have to do is create an instance of the model, and call its fit method while passing in the training set:
svm = SVM()
svm.fit(X_train, y_train)After training is complete, we can test the model to see how it performs:
predictions = svm.predict(np.array(X_test))
predictions = np.argmax(predictions, axis=1)
accuracy = np.mean(predictions == y_test)
print(f"Accuracy: {accuracy}")Upon running that, I typically get an accuracy of ~90%. Pretty good, considering we are classifying fish into 9 species based only on their length, weight, and length-to-weight ratio. It is apparent that the model is not guessing, but is actually recognizing patterns and using the to identify the fish.
Let’s take a closer look at the training progress of the model, to see how descending the gradient helped us. Using this code, I can plot the loss of the model and its accuracy on the training set vs epochs:
# prompt: plot the history of the sv object against epochs
import matplotlib.pyplot as plt
# Extract loss and accuracy from the history
epochs = [entry['epoch'] for entry in svm.history]
losses = [entry['loss'] for entry in svm.history]
accuracies = [entry['accuracy'] for entry in svm.history]
# Plot the loss
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(epochs, losses)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss vs. Epochs')
# Plot the accuracy
plt.subplot(1, 2, 2)
plt.plot(epochs, accuracies)
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Accuracy vs. Epochs')
plt.tight_layout()
plt.show()We expect this code to yield two graphs: one that shows loss decreasing over the epochs, and another that shows accuracy increasing over the epochs. The rate of change should be steepest at the beginning, and then taper of as we approach the optimal set of parameters. Here is what we get:
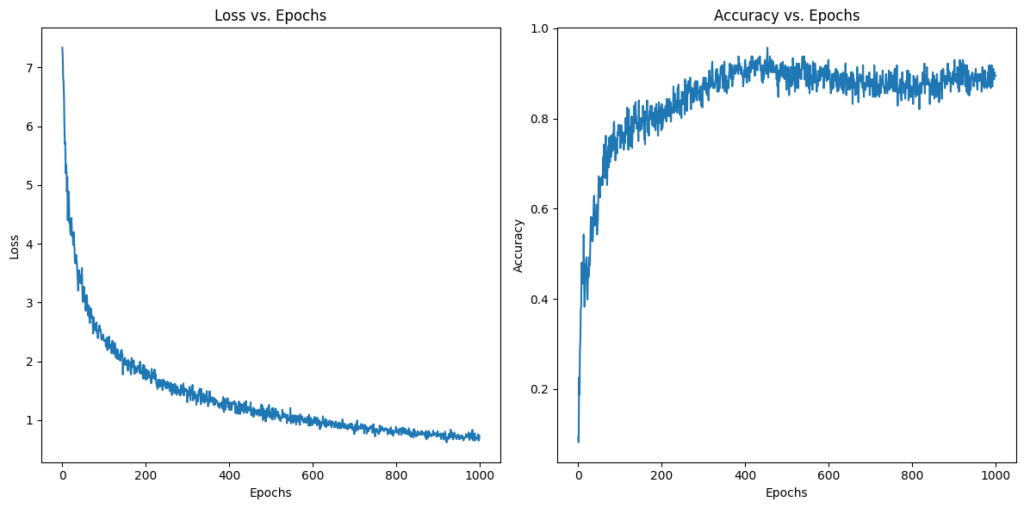
Just what we expected! This is further evidence that our implementation is working properly!
Finding the Best Hyperparameters
So, now we have a working classifier. But we are not done yet! Remember that we made three subdivisions of the data: training, testing, and validation. We have not used the validation set yet!
The validation set is used to find the optimal values for our hyperparameters. Hyperparameters are constant values in our model that are not changed in the training process. Examples from our classifier are the number of epochs, the batch size, and the learning rate. We will use our validation set to find optimal values for these hyperparameters.
Testing Hyperparameters with the Validation Set
Typically, the way validation of hyperparameters works is: first, create a set of values of the hyperparameters to test. Then, train a model on the test set using those each of the hyperparameter values. After that, evaluate its performance on the validation set. The hyperparameters that yield the lowest loss are the optimal hyperparameters, so they are the ones that should be used for the model moving forward.
I decided to validate the learning rate and batch size of my classifier. In code, that looked like
lrs = [1e-1, 1e-2, 1e-3, 1e-4, 1e-5]
batch_sizes = [16, 32, 64, 128, 256]
best_loss = np.inf
best_hyperparameters = None
svms = []
for lr in lrs:
for batch_size in batch_sizes:
#fit an SVM to the training data
svm = SVM()
svm.fit(X_train, y_train, epochs=1000, batch_size=batch_size, lr=lr, verbose=False)
#evaluate it on the validation set
val_pred = svm.predict(np.array(X_val))
loss = svm.loss(np.array(val_pred), np.array(y_val))
#save the hyperparemeter values, if the loss is lower
if loss < best_loss:
best_loss = loss
best_hyperparameters = (lr, batch_size)
#save the svm to the list
svms.append({
'svm': svm,
'lr': lr,
'batch_size': batch_size,
'loss': loss
})
print(f"Best hyperparameters: {best_hyperparameters}")
print(f"Best loss: {best_loss}")This code tries every possible combination of the provided learning rates and batch sizes by training a model an passing the values into the fit function. Just for fun, I decided to plot the loss and accuracy through the epochs all together, to see how they compare:
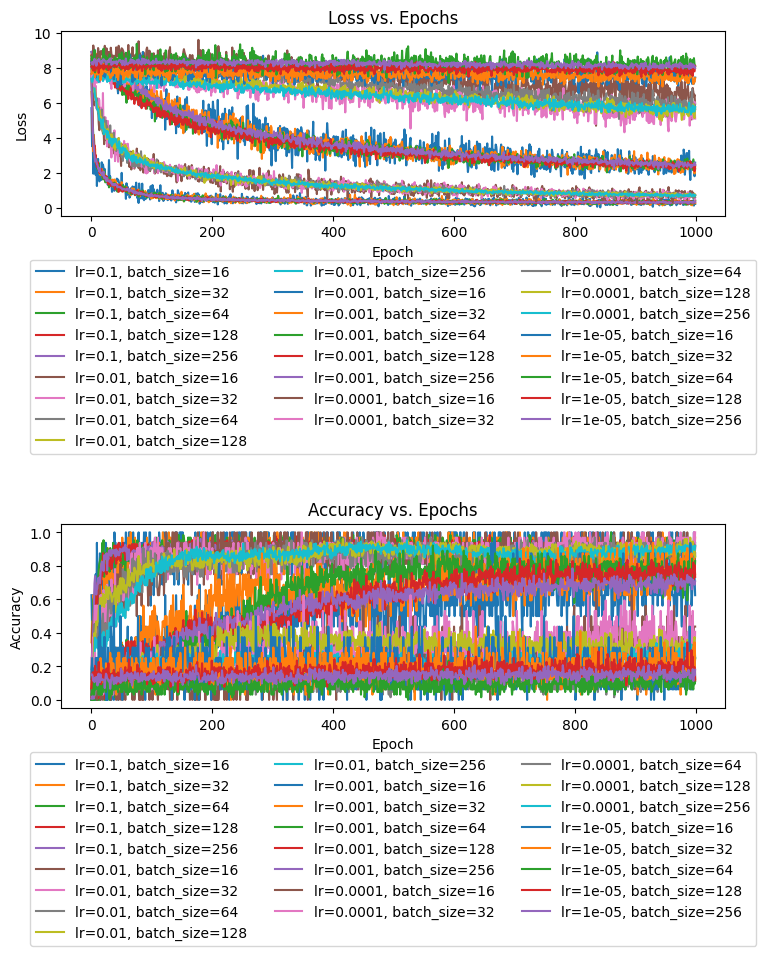
It is obviously a little tough to read due to repeated colors, but we can still gain some insights. Across 1000 epochs, the models’ progressed in tight packs based on their learning rate, with a higher learning rate leading to a much faster convergence on the minimum loss value. 0.1 proved to be the best learning rate across 1000 epochs, though with a larger number of epochs, the models with a learning rate of 0.01 likely would have caught up. The slower learning rates were progressing, but their slower speed of convergence shows them to be suboptimal learning rate values.
Meanwhile, if we look closer at the groupings in the graph, we can see the batch size come into play. The smaller the batch size, the more erratically the loss function appeared to fluctuate up and down. This makes sense, because with a smaller batch size, there is a greater chance of the step we take not generalizing well to the rest of the training set. So, we would expect a larger batch size to produce smaller fluctuations. But, smaller batches also help the training process to go faster, so there is a bit of a trade-off here. The differences among batch sizes, are relatively minor, as the batch sizes I tested do not overpower the downward trend the weights produce.
It is also interesting to observe how there is a sort of inverse relationship between accuracy and loss, but there is no direct correlation. Accuracy tends to increase as loss decreases, and we can see the groupings of the accuracy lines around learning rates, but we can tell from the graphs that the two metrics do not move in direct synchronization. If they did, we would see much tighter groupings in the accuracy graph.
Best Hyperparameter Results
In practice, the best hyperparameters in my notebook consistently come out with a learning rate of 0.1, while the batch size varies, usually coming out as 32 or 64. The last thing to do is see the effects of these optimal hyperparameters in action on the test set:
svm_best = SVM()
svm_best.fit(X_train, y_train, batch_size=best_hyperparameters[1], lr=best_hyperparameters[0])
svm_default = SVM()
svm_default.fit(X_train, y_train)
best_preds = svm_best.predict(np.array(X_test))
default_preds = svm_default.predict(np.array(X_test))
best_loss = svm_best.loss(np.array(best_preds), np.array(y_test))
default_loss = svm_default.loss(np.array(default_preds), np.array(y_test))
best_accuracy = np.mean(np.argmax(best_preds, axis=1) == y_test)
default_accuracy = np.mean(np.argmax(default_preds, axis=1) == y_test)
print(f"Best loss: {best_loss}")
print(f"Default loss: {default_loss}")
print(f"Difference: {best_loss - default_loss}")
print("---------------------")
print(f"Best accuracy: {best_accuracy}")
print(f"Default accuracy: {default_accuracy}")
print(f"Difference: {best_accuracy - default_accuracy}")The default hyperparameters are just the default values of the keyword arguments, so batch_size = 256 and lr = 0.01.
Here is the result from one running of this code:
Best loss: 0.30238443639665574
Default loss: 0.7224593163043828
Difference: -0.420074879907727
---------------------
Best accuracy: 0.9080882352941176
Default accuracy: 0.8946078431372549
Difference: 0.013480392156862697As you can see, we get the loss to drop quite a bit lower by using the optimal hyperparameters. This also results in a small but meaningful improvement to our accuracy.
Nice! By using our validation set to tune our hyperparameters, we are able to further improve our model’s performance on the test set.
Conclusion
Through the hard brainwork of implementing this SVM Multi-classifier from scratch, we gained a massive amount of new knowledge! We learned how to build model that can classify examples into more than two groups! We also successfully implemented the bias trick to fold the bias term in with the weights. Most importantly, we implemented gradient descent from scratch using only vanilla python and numpy to train our model. Finally, we validated our hyperparameters using the validation set to further boost our model’s performance.
All of this was in service of building a model that can identify which species out of 9 options a fish specimen belongs to based on nothing more than their length and weight! The model shown here achieves this goal admirably, with out optimal model identifying the fish with greater than 90% accuracy. To gain more insights into how this classifier works, feel free to check out my Colab notebook by clicking here. With the knowledge we gained here, we are well on our way to becoming machine learning pros! Thank you for reading!

Leave a Reply